Topological indistinguishability
In topology, two points of a topological space X are topologically indistinguishable if they have exactly the same neighborhoods. That is, if x and y are points in X, and A is the set of all neighborhoods that contain x, and B is the set of all neighborhoods that contain y, then x and y are "topologically indistinguishable" if and only if A = B.
Intuitively, two points are topologically indistinguishable if the topology of X is unable to discern between the points.
Two points of X are topologically distinguishable if they are not topologically indistinguishable. This means there is an open set containing precisely one of the two points (equivalently, there is a closed set containing precisely one of the two points). This open set can then be used to distinguish between the two points. A T0 space is a topological space in which every pair of distinct points is topologically distinguishable. This is the weakest of the separation axioms.
Topological indistinguishability defines an equivalence relation on any topological space X. If x and y are points of X we write x ≡ y for “x and y are topologically indistinguishable”. The equivalence class of x will be denoted by [x].
Contents |
Examples
For T0 spaces (in particular, for Hausdorff spaces) the notion of topological indistinguishability is trivial, so one must look to non-T0 spaces to find interesting examples. On the other hand, regularity and normality do not imply T0, so we can find examples with these properties. In fact, almost all of the examples given below are completely regular.
- In an indiscrete space, any two points are topologically indistinguishable.
- In a pseudometric space, two points are topologically indistinguishable if and only if the distance between them is zero.
- In a seminormed vector space, x ≡ y if and only if ‖x − y‖ = 0.
- For example, let L2(R) be the space of all measurable functions from R to R which are square integrable (see Lp space). Then two functions f and g in L2(R) are topologically indistinguishable if and only if they are equal almost everywhere.
- In a topological group, x ≡ y if and only if x−1y ∈ cl{e} where cl{e} is the closure of the trivial subgroup. The equivalence classes are just the cosets of cl{e} (which is always a normal subgroup).
- Uniform spaces generalize both pseudometric spaces and topological groups. In a uniform space, x ≡ y if and only if the pair (x, y) belongs to every entourage. The intersection of all the entourages is an equivalence relation on X which is just that of topological indistinguishability.
- Let X have the initial topology with respect to a family of functions
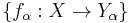 . Then two points x and y in X will be topologically indistinguishable if the family
. Then two points x and y in X will be topologically indistinguishable if the family 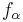 does not separate them (i.e.
does not separate them (i.e.  for all
for all  ).
). - Given any equivalence relation on a set X there is a topology on X for which the notion of topological indistinguishability agrees with the given equivalence relation. One can simply take the equivalence classes as a base for the topology. This is called the partition topology on X.
Specialization preorder
The topological indistinguishability relation on a space X can be recovered from a natural preorder on X called the specialization preorder. For points x and y in X this preorder is defined by
- x ≤ y if and only if x ∈ cl{y}
where cl{y} denotes the closure of {y}. Equivalently, x ≤ y if the neighborhood system of x, denoted Nx, is contained in the neighborhood system of y:
- x ≤ y if and only if Nx ⊂ Ny.
It is easy to see that this relation on X is reflexive and transitive and so defines a preorder. In general, however, this preorder will not be antisymmetric. Indeed, the equivalence relation determined by ≤ is precisely that of topological indistinguishability:
- x ≡ y if and only if x ≤ y and y ≤ x.
A topological space is said to be symmetric (or R0) if the specialization preorder is symmetric (i.e. x ≤ y implies y ≤ x). In this case, the relations ≤ and ≡ are identical. Topological indistinguishability is better behaved in these spaces and easier to understand. Note that this class of spaces includes all regular and completely regular spaces.
Properties
Equivalent conditions
There are several equivalent ways of determining when two points are topologically indistinguishable. Let X be a topological space and let x and y be points of X. Denote the respective closures of x and y by cl{x} and cl{y}, and the respective neighborhood systems by Nx and Ny. Then the following statements are equivalent:
- x ≡ y
- for each open set U in X, either U contains both x and y or neither of them
- Nx = Ny
- x ∈ cl{y} and y ∈ cl{x}
- cl{x} = cl{y}
- x ∈ ∩Ny and y ∈ ∩Nx
- ∩Nx = ∩Ny
- x ∈ cl{y} and x ∈ ∩Ny
- x belongs to every open set and every closed set containing y
- a net or filter converges to x if and only if it converges to y
These conditions can be simplified in the case where X is symmetric space. For these spaces (in particular, for regular spaces), the following statements are equivalent:
- x ≡ y
- for each open set U, if x ∈ U then y ∈ U
- Nx ⊂ Ny
- x ∈ cl{y}
- x ∈ ∩Ny
- x belongs to every closed set containing y
- x belongs to every open set containing y
- every net or filter that converges to x converges to y
Equivalence classes
To discuss the equivalence class of x, it is convenient to first define the upper and lower sets of x. These are both defined with respect to the specialization preorder discussed above.
The lower set of x is just the closure of {x}:
while the upper set of x is the intersection of the neighborhood system at x:
The equivalence class of x is then given by the intersection
Since ↓x is the intersection of all the closed sets containing x and ↑x is the intersection of all the open sets containing x, the equivalence class [x] is the intersection of all the open and closed sets containing x.
Both cl{x} and ∩Nx will contain the equivalence class [x]. In general, both sets will contain additional points as well. In symmetric spaces (in particular, in regular spaces) however, the three sets coincide:
In general, the equivalence classes [x] will be closed if and only if the space is symmetric.
Continuous functions
Let f : X → Y be a continuous function. Then for any x and y in X
- x ≡ y implies f(x) ≡ f(y).
The converse is generally false (There are quotients of T0 spaces which are trivial). The converse will hold if X has the initial topology induced by f. More generally, if X has the initial topology induced by a family of maps 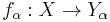 then
then
- x ≡ y if and only if fα(x) ≡ fα(y) for all α.
It follows that two elements in a product space are topologically indistinguishable if and only if each of their components are topologically indistinguishable.
Kolmogorov quotient
Since topological indistinguishability is an equivalence relation on any topological space X, we can form the quotient space KX = X/≡. The space KX is called the Kolmogorov quotient or T0 identification of X. The space KX is, in fact, T0 (i.e. all points are topologically distinguishable). Moreover, by the characteristic property of the quotient map any continuous map f : X → Y from X to a T0 space factors through the quotient map q : X → KX.
Although the quotient map q is generally not a homeomorphism (since it is not generally injective), it does induce a bijection between the topologies of X and the topologies of KX. Intuitively, the Kolmogorov quotient does not alter the topology of a space. It just reduces the point set until points become topologically distinguishable.
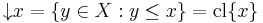
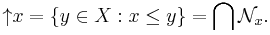
![[x] = {\mathop{\darr}x} \cap {\mathop{\uarr}x}.](/2012-wikipedia_en_all_nopic_01_2012/I/d42f13b06f9b34079d8dfea90753f208.png)
![[x] = \textrm{cl}\{x\} = \bigcap\mathcal{N}_x.](/2012-wikipedia_en_all_nopic_01_2012/I/806b88d0f814fff0516c150045b00518.png)